在使用代數資料型態定義(或說是模擬)了清單類型之後,我們回到 Java 開發者的函數式程式設計(2) 中留下的最後一個問題。現在我們寫的是 Java,該怎麼將以下的程式碼改寫為 Java?
sum [] = 0
sum (x:xs) = x + sum xsif 條件判斷來檢查清單物件是不是 Nil,因此可以如下定義一個 sum 方法:
public static Integer sum(List<Integer> lt) {
if(lt == Nil) return 0;
else return lt.head() + sum(lt.tail());
}sum 方法之後,sum(list(1, 2, 3, 4, 5)) 就會傳回 15 的結果,看起來還不錯,接著想想看,怎麼定義一個 addOne 方法,可以對傳入清單中每個元素加一後傳回新清單呢?這個問題的其中一個子問題是,如果是空清單的話,結果會傳回什麼?就只是一個空清單!另一個子問題是,如果傳入的清單中,首元素為 x 而尾清單為 xs,要怎麼計算傳回的結果?對 x 加一,然後使用 xs 再次呼叫 addOne 方法,接著使用 con 方法將兩者的結果組為一個新清單。使用 Java 來描述這兩個子問題的話,結果會如下:
public static List<Integer> addOne(List<Integer> lt) {
if(lt == Nil) return nil();
else return cons(lt.head() + 1, addOne(lt.tail()));
}(+ 1) 的部份改為 (- 2),而方法名稱 addOne 改為 subtractTWO。如果想將清單中每個元素乘 3 後傳回新清單,則只要將程式碼中 (+ 1) 改為 (* 3),並將方法名稱 addOne 改為 multiplyByThree。看出什麼了嗎?如果 (+ 1)、(- 2) 與 (* 3) 是可傳入的一級函式(First-class function),那麼這個程式碼流程樣版就可以重用,嗯?JDK8 的 Lambda 要導入的不就是一級函式?我們可以定義一個函式介面(Functional interface)如下:
public interface F1<P, R> {
R apply(P p);
}map 方法來做這個處理。
public class AlgebraicType {
...
public static <T, R> List<R> map(List<T> lt, F1<T, R> f) {
if(lt == Nil) return nil();
return cons(f.apply(lt.head()), map(lt.tail(), f));
}
}map(list(1, 2, 3, 4, 5), x -> x + 1);map(list(1, 2, 3, 4, 5), x -> x - 2);map(list(1, 2, 3, 4, 5), x -> x * 3);map 方法很有用,可以有一百萬種使用方式。類似地,如果想將清單中大於 3 的元素過濾出來成為新清單呢?我們可以寫下如下的程式碼:
public static List<Integer> greaterThanThree(List<Integer> lt) {
if(lt == Nil) return nil();
else {
if(lt.head() > 3) {
return cons(lt.head(), greaterThanThree(lt.tail()));
}
else {
return greaterThanThree(lt.tail());
}
}
}public static List<Integer> smallerThanTen(List<Integer> lt) {
if(lt == Nil) return nil();
else {
if(lt.head() < 10) {
return cons(lt.head(), smallerThanTen(lt.tail()));
}
else {
return smallerThanTen(lt.tail());
}
}
}filter 方法來做這件事:
public class AlgebraicType {
...
public static <T> List<T> filter(List<T> lt, F1<T, Boolean> f) {
if(lt == Nil) return nil();
else {
if(f.apply(lt.head())) {
return cons(lt.head(), filter(lt.tail(), f));
}
else {
return filter(lt.tail(), f);
}
}
}
}filter(list(1, 2, 3, 4, 5), x -> x > 3);filter(list(10, 19, 3, 4, 5), x -> x < 10);filter 方法很有用,可以有一百萬種過濾方式。類似地,逐步消減清單元素以獲得某個值也是個常見模式,在定義處理用的方法之前,先來定義一個函式介面:
public interface F2 {
R apply(R r, P p);
}reduce 方法:
public class AlgebraicType {
...
public static <T, R> R reduce(List<T> lt, F2<T, R> f, R r) {
if(lt == Nil) return r;
else {
return reduce(lt.tail(), f, f.apply(r, lt.head()));
}
}
}reduce(list(1, 2, 3, 4, 5), (sum, x) -> sum + x, 0);reduce 方法到底變了什麼把戲不是件容易的事。reduce 方法有時也稱為 foldLeft,它做的事情,就像是從左開始折紙一樣,reduce(list(1, 2, 3, 4, 5), (sum, x) -> sum + x, 0) 做的事情就如同以下的動畫一樣,一邊折紙,一邊將左邊的數字加到右邊,在完成折紙的動作之後,就可以得到最後的結果。
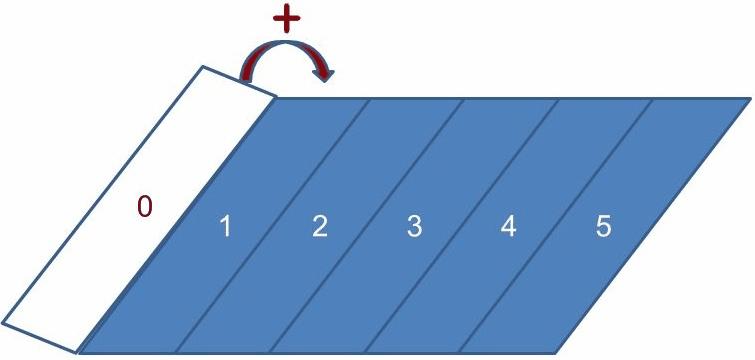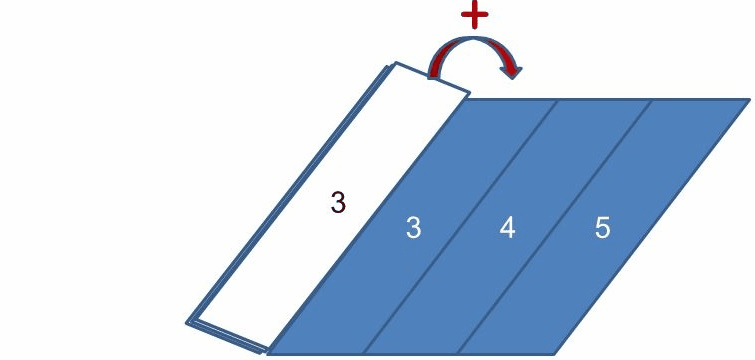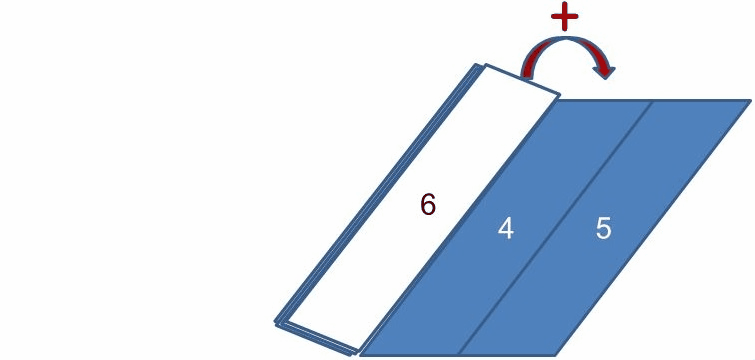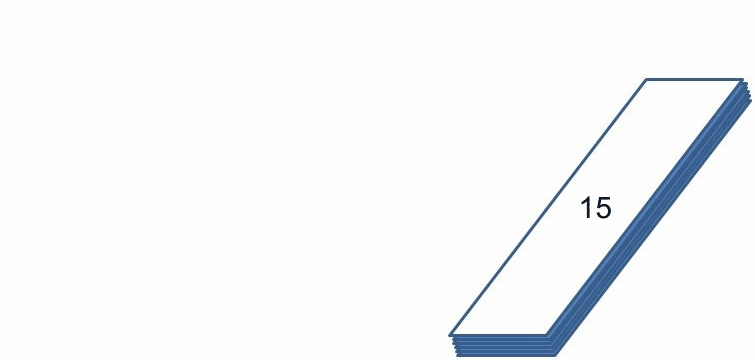
reduce 方法很有用,可以有一百萬中消減清單元素以求值的方式。然而,這邊的重點在於,如果以函數式風格來編寫程式,你會很容易發覺函式間具有相近結構,因而能輕易地提煉為更高階的抽象以進行重用,這邊提到的
filter、map 與 reduce 就是個不錯的例子。一旦你能夠函數式地思考,你就能夠發現更多高階的抽象。
