如果曲面的函式為顯函式y = f(x, z)的形式,則其法線向量可以經由以下的偏微分方程式求得:
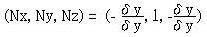
如果曲面的函式為隱函式的形式,必須先求得其參數式,再對參數式經由以下的偏微分方程式求得法線向量:

方線向量使用的一個例子是求受光量,將每一個點帶入方程式,求得法向量並與光線向量進行內積運算,如此就可以求得受光量,並將其對應至陰影色譜中適當的顏色,在繪製時我們由最遠的點開始繪製,如此近的點在繪製時將會遮蓋住遠的點,如此就可以處理掉深度的問題。
為了適當的表現出陰影的效果,所繪製的點必須有一定的密度,也就使用掉不少運算資源,可以使用法線向量判定法,將Z軸為負的部份過濾掉不畫,因為這些點在背部,本來將看不到,可以節省掉這些點的繪製成本。

