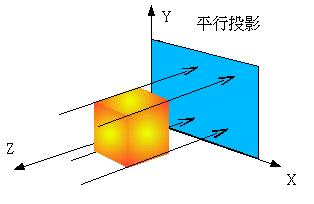
想像將一個物體以平行光線照射,此時投影在XY平面上的座標點是沒有遠近感的,簡單的說,就是將座標的Z分量省略,如下圖所示:
如果想要創造物體的遠近感,必須使用非平行光來照射物體,此時投射在XY平面的點會因比例的關係,而使得每一個點在XY平面上投影時彼此靠近,因而造成具有遠近的感覺:
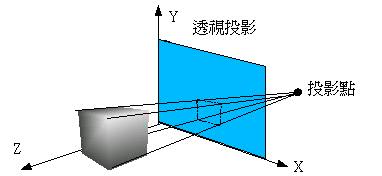
這種方法稱之為透視法,您的投影點設的越遠,遠近感就越顯著,而您觀察物體的位置(相當於此例中的光源位置,或反過來說是投影點的位置)也會影響透視的結果,為了導證公式方便,將投影點設定在Z軸上,若空間中有一點(x,y,z),則先看看XZ平面上的座標變化:
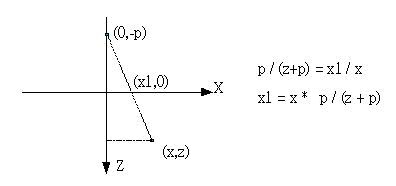
公式的導證只使用簡單的相似三角形關係就可以得到,同樣的,可以看看YZ平面上的座標變化:
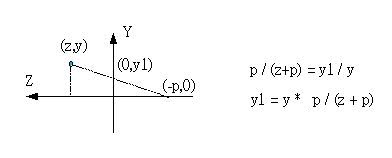
使用以上的公式,再配合座標旋轉公式,您就可以對立體物件的頂點作各種轉換的動作,當然物件的頂點就決定了3D圖的基本,這意味了您可以藉此創造一些簡單的3D圖形。

