假設三維空間中有一點為(x, y, z),它分別繞直角座標的軸作旋轉,如下圖所示:
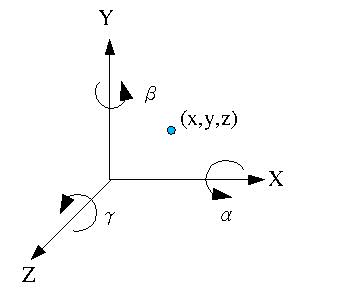
旋轉時假設若座標軸正方向朝自己,我們定義旋轉時逆時針為正轉,若分別繞三個軸旋轉後的座標為(x3, y3, z3),這邊將介紹中間的公式轉換導證。
必須知道兩個基本的三角函式公式:
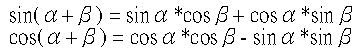
現在假設先繞Y軸旋轉,所以此時y座標是不變的,來看x與z座標如何變化,假設點投射於X-Z平面上的長度為L,則可以如下推導公式:
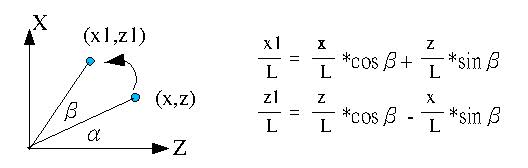
將L消去,可以得到繞Y軸旋轉後的公式如下:
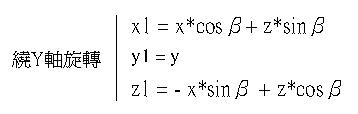
依照以上相同的方法,分別對X軸與Z軸作旋轉,可以得到中間的轉換公式:
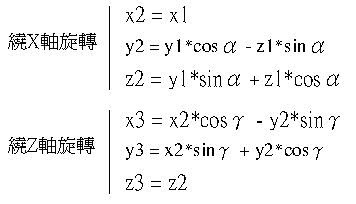
如果是在電腦上繪圖,如果直接將座標投射至X-Y平面,所以公式中的部份Z座標是可以省略不計算的,也就是z2與z3的部份,所以最後得到的公式是:


