不知道該如何稱這個主題,就先叫作「太空船座標旋轉」好了。
簡單的說,就是當您位於一個太空船中原地打轉,由窗戶中所看到的物體座標轉換,事實上物體的位置是不變的,變的是太空船的座標軸,假設在太空船中所看到的 原來物體座標為(x,y),太空船旋轉α徑度後,物體相對於太空船座標軸的座標為(x1,y1),如下圖所示:
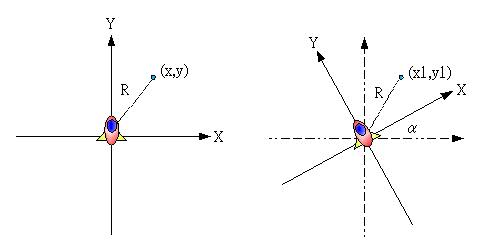
在計算(x,y)與(x1,y1)之間的關係前,仍然需要下面這兩個三角函式:
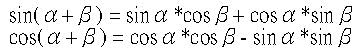
假設太空船與物體的距離為R,由於是原地打轉,所以R是不變的,假設物體與太空船的X座標軸夾角為β,如下所示:
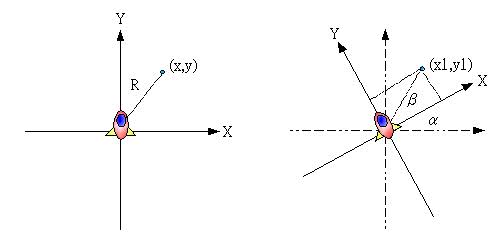
由上圖,α+β其實就是旋轉前的X軸與物體的夾角,所以配合之前的三角函式,可以導出以下的關係:
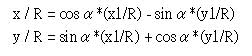
將R消去並解聯立方程式,(x,y)與(x1,y1)的關係就可以導出,解聯立的這個部份就不列出了。

