由於旋轉體、錐狀體、柱狀體的幾何性質,使得它們的頂點配置具有規則而容易以運算來進行配置,觀念上十分簡單。
旋轉體
假設旋轉體是繞著Y軸旋轉,則可以先定義出一條錂線上的頂點,與它們各自距Y軸的距離,接下來只要旋轉這些頂點,就可以得出旋轉體所有的頂點,如下所示: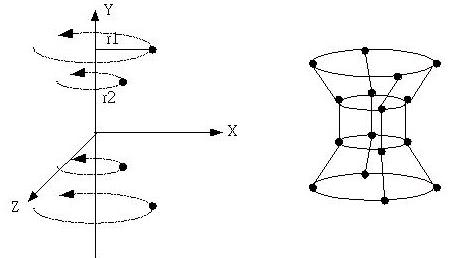
真實世界中的旋轉體很多,所以這個方法可以畫出各種不同的旋轉體;下面這個程式畫出一個高腳杯,它不儲存頂點,而直接利用運算後的頂點來繪製酒杯的骨架,採取的方法是先用迴圈畫圈圈,再由一次迴圈來畫錂線:
- Demo.java
package cc.openhome;
import java.awt.Color;
import java.awt.Graphics;
import javax.swing.JApplet;
import static java.lang.Math.*;
public class Demo extends JApplet {
private final static double[] Y_LOCATIONS =
{180, 140, 100, 60, 20, 10, 4, 0};
private final static double[] R_DISTANCES =
{100, 55, 10, 10, 10, 50, 80, 80};
private int orgX;
private int orgY;
public void init() {
super.init();
setBackground(Color.black);
setSize(300, 300);
orgX = getWidth() / 3;
orgY = getHeight() - 80;
}
public void paint(Graphics g) {
g.setColor(Color.yellow);
drawCircle(g);
drawLine(g);
}
private void drawCircle(Graphics g) {
// 360 度畫圈
for (int i = 0; i < Y_LOCATIONS.length; i++) {
// 我們要畫線段,所以求出第一點不用畫
double x = R_DISTANCES[i] * cos(0);
double z = R_DISTANCES[i] * sin(0);
int startX = orgX + xAfterRotateAroundXZ(x, Y_LOCATIONS[i], z);
int startY = orgY - yAfterRotateAroundXZ(x, Y_LOCATIONS[i], z);
for (int j = 1; j <= 360; j += 10) {
// 計算 x, z 座標
x = R_DISTANCES[i] * cos(toRadians(j));
z = R_DISTANCES[i] * sin(toRadians(j));
// 立體旋轉,從斜角繪製,調整繪圖中心至視窗中心
int endX = orgX + xAfterRotateAroundXZ(x, Y_LOCATIONS[i], z);
int endY = orgY - yAfterRotateAroundXZ(x, Y_LOCATIONS[i], z);
g.drawLine(startX, startY, endX, endY);
startX = endX;
startY = endY;
}
}
}
private void drawLine(Graphics g) {
// 畫錂線
for (int j = 0; j <= 360; j += 60) {
// 我們要畫線段,所以求出第一點不用畫
double x = R_DISTANCES[0] * cos(toRadians(j));
double z = R_DISTANCES[0] * sin(toRadians(j));
int startX = orgX + xAfterRotateAroundXZ(x, Y_LOCATIONS[0], z);
int startY = orgY - yAfterRotateAroundXZ(x, Y_LOCATIONS[0], z);
for (int i = 1; i < Y_LOCATIONS.length; i++) {
x = R_DISTANCES[i] * cos(toRadians(j));
z = R_DISTANCES[i] * sin(toRadians(j));
// 立體旋轉,從斜角繪製,調整繪圖中心至視窗中心
int endX = orgX + xAfterRotateAroundXZ(x, Y_LOCATIONS[i], z);
int endY = orgY - yAfterRotateAroundXZ(x, Y_LOCATIONS[i], z);
g.drawLine(startX, startY, endX, endY);
startX = endX;
startY = endY;
}
}
}
private int xAfterRotateAroundXZ(double x, double y, double z) {
// 從斜角繪製
// 繞 x 軸轉 30 度,繞 z 軸轉 -25 度
double rotateX = toRadians(30);
double rotateZ = toRadians(-25);
return (int) (x * cos(rotateZ) -
(y * cos(rotateX) - z * sin(rotateX)) * sin(rotateZ));
}
private int yAfterRotateAroundXZ(double x, double y, double z) {
// 從斜角繪製
// 繞 x 軸轉 30 度,繞 z 軸轉 -25 度
double rotateX = toRadians(30);
double rotateZ = toRadians(-25);
return (int) (x * sin(rotateZ) +
(y * cos(rotateX) - z * sin(rotateX)) * cos(rotateZ));
}
}以下是使用HTML5 Canvas的方式(如果瀏覽器支援HTML5 Canvas,例如最新版的Firexfox、Chrome、IE9等,可以直接將下面的內容存為HTML或按下檔名連結,直接載入瀏覽器執行觀看結果:
<!DOCTYPE html>
<html>
<head>
<meta content="text/html; charset=Big5" http-equiv="content-type">
<script type="text/javascript">
window.onload = function() {
function toRadians(angle) {
return angle * Math.PI / 180;
}
var sin = Math.sin;
var cos = Math.cos;
var sqrt = Math.sqrt;
function xAfterRotateAroundXZ(x, y, z) {
// 從斜角繪製
// 繞 x 軸轉 30 度,繞 z 軸轉 -25 度
var rotateX = toRadians(30);
var rotateZ = toRadians(-25);
return parseInt(x * cos(rotateZ) -
(y * cos(rotateX) - z * sin(rotateX)) * sin(rotateZ));
}
function yAfterRotateAroundXZ(x, y, z) {
// 從斜角繪製
// 繞 x 軸轉 30 度,繞 z 軸轉 -25 度
var rotateX = toRadians(30);
var rotateZ = toRadians(-25);
return parseInt(x * sin(rotateZ) +
(y * cos(rotateX) - z * sin(rotateX)) * cos(rotateZ));
}
var Y_LOCATIONS = [180, 140, 100, 60, 20, 10, 4, 0];
var R_DISTANCES = [100, 55, 10, 10, 10, 50, 80, 80];
var canvas1 = document.getElementById('canvas1');
var orgX = canvas1.width / 3;
var orgY = canvas1.height - 80;
var context = canvas1.getContext('2d');
context.beginPath();
// 360 度畫圈
for(var i = 0; i < Y_LOCATIONS.length; i++) {
// 我們要畫線段,所以求出第一點不用畫
var x = R_DISTANCES[i] * cos(0);
var z = R_DISTANCES[i] * sin(0);
var startX = orgX + xAfterRotateAroundXZ(
x, Y_LOCATIONS[i], z);
var startY = orgY - yAfterRotateAroundXZ(
x, Y_LOCATIONS[i], z);
context.moveTo(startX, startY);
for(var j = 1; j <= 360; j += 10) {
// 計算 x, z 座標
x = R_DISTANCES[i] * cos(toRadians(j));
z = R_DISTANCES[i] * sin(toRadians(j));
// 立體旋轉,從斜角繪製,調整繪圖中心至視窗中心
var endX = orgX + xAfterRotateAroundXZ(
x, Y_LOCATIONS[i], z);
var endY = orgY - yAfterRotateAroundXZ(
x, Y_LOCATIONS[i], z);
context.lineTo(endX, endY);
}
}
// 畫錂線
for(var j = 0; j <= 360; j += 60) {
// 我們要畫線段,所以求出第一點不用畫
var x = R_DISTANCES[0] * cos(toRadians(j));
var z = R_DISTANCES[0] * sin(toRadians(j));
var startX = orgX + xAfterRotateAroundXZ(
x, Y_LOCATIONS[0], z);
var startY = orgY - yAfterRotateAroundXZ(x,
Y_LOCATIONS[0], z);
context.moveTo(startX, startY);
for(var i = 1; i < Y_LOCATIONS.length; i++) {
x = R_DISTANCES[i] * cos(toRadians(j));
z = R_DISTANCES[i] * sin(toRadians(j));
// 立體旋轉,從斜角繪製,調整繪圖中心至視窗中心
var endX = orgX + xAfterRotateAroundXZ(x,
Y_LOCATIONS[i], z);
var endY = orgY - yAfterRotateAroundXZ(x,
Y_LOCATIONS[i], z);
context.lineTo(endX, endY);
}
}
context.stroke();
context.closePath();
};
</script>
</head>
<body>
<canvas id="canvas1" width="300" height="300"></canvas>
</body>
</html>
在Firefox下的效果如下:
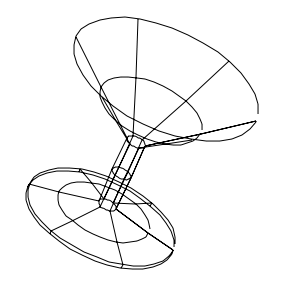
錐狀體
錐狀體將底面所有的頂點放置在XZ平面上,底面與錐頂點的交點為(xc, 0, yc),高度為h,則錐頂點的座標為(xc, h, yc),如下所示: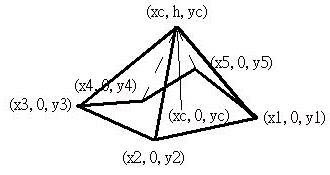
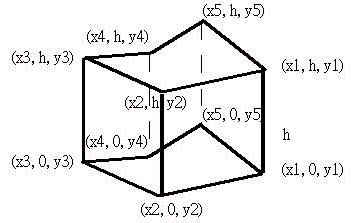
柱狀體
柱狀體將底面所有的頂點放置在XZ平面上,高度為h,則頂點座標配置如下所示: