I talked about spirals in previous documents, such as Golden spiral and Archimedean spiral. I used equations to figure out points on the spirals' path and then connect.

You can use turtle graphics to create spirals, too. Imagine you are forwarding and turning a turtle with different lengths and angles. The turtle will leave footprints on the path it crawled. Turtle Spiral Generator is such a customizer.

Forwarding and turning

Using a turtle to create a spiral is easy. Just forward it leng distance and turn angle continuously. If you remain leng unchanged and let angle = 90, the turtle will draw a square. If angle is 120, it will draw a triangle. What will it draw if angle is 144?

function turtle(x, y, angle) = [[x, y], angle];

function get_x(turtle) = turtle[0][0];
function get_y(turtle) = turtle[0][1];
function get_xy(turtle) = turtle[0];
function get_angle(turtle) = turtle[1];

function set_point(turtle, point) = [point, get_angle(turtle)];

function set_x(turtle, x) = [[x, get_y(turtle)], get_angle(turtle)];
function set_y(turtle, y) = [[get_x(turtle), y], get_angle(turtle)];
function set_angle(turtle, angle) = [get_xy(turtle), angle];

function forward(turtle, leng) = 
    turtle(
        get_x(turtle) + leng * cos(get_angle(turtle)), 
        get_y(turtle) + leng * sin(get_angle(turtle)), 
        get_angle(turtle)
    );

function turn(turtle, angle) = [get_xy(turtle), get_angle(turtle) + angle];

module line(point1, point2, width = 1, cap_round = true) {
    angle = 90 - atan((point2[1] - point1[1]) / (point2[0] - point1[0]));
    offset_x = 0.5 * width * cos(angle);
    offset_y = 0.5 * width * sin(angle);

    offset1 = [-offset_x, offset_y];
    offset2 = [offset_x, -offset_y];

    if(cap_round) {
        translate(point1) circle(d = width, $fn = 24);
        translate(point2) circle(d = width, $fn = 24);
    }

    polygon(points=[
        point1 + offset1, point2 + offset1,  
        point2 + offset2, point1 + offset2
    ]);
}

module polyline(points, width = 1) {
    module polyline_inner(points, index) {
        if(index < len(points)) {
            line(points[index - 1], points[index], width);
            polyline_inner(points, index + 1);
        }
    }

    polyline_inner(points, 1);
}

// The above is the implementation of turtle graphics.

side_leng = 10;
angle = 144;
width = 1;

t1 = turtle(0, 0, 0);

t2 = forward(t1, side_leng);
polyline([get_xy(t1), get_xy(t2)], width);

t3 = forward(turn(t2, angle), side_leng);
polyline([get_xy(t2), get_xy(t3)], width);

t4 = forward(turn(t3, angle), side_leng);
polyline([get_xy(t3), get_xy(t4)], width);

t5 = forward(turn(t4, angle), side_leng);
polyline([get_xy(t4), get_xy(t5)], width);

t6 = forward(turn(t5, angle), side_leng);
polyline([get_xy(t5), get_xy(t6)], width);

The result is a star (pentagram). Its internal angle is 36 degrees. If you take 36 from 180, you get 144.

Recursion

Of course, writing the above code looks stupid. You cannot, however, use a loop here because OpenSCAD is Functional programming. If you need repetition, recursion is the solution.

// omitted..require turtle graphics implementation

module turtle_spiral(t_before, times, side_leng, angle, width) {
    if(times != 0) {
        t_after = forward(turn(t_before, angle), side_leng);
        polyline([get_xy(t_before), get_xy(t_after)], width);
        turtle_spiral(t_after, times - 1, side_leng, angle, width);
    }

}

side_leng = 10;
angle = 144;
width = 1;
times = 5;

turtle_spiral(turtle(0, 0, 0), times, side_leng, angle, width);

When seeing for the first time, you might think recursion troublesome or hard. In fact, nothing. If you start to feel annoying or hard, it's probably you are tracing too many variables. That might be a signal that you have too many tasks on each recursion. That's a common mistake when writing code in imperative languages.

It's easier to do recursion in Functional programming languages because variables and vectors are immutable. It forces you to do only one thing in the function so that you can observe repetitive tasks easily. Take the above pentagram for example. You can easily find the repetitive work in the code.

t_after = forward(turn(t_before, angle), side_leng);
polyline([get_xy(t_before), get_xy(t_after)], width);

You just have to do this task in the module. What's the next task? Don't care. Just invoke the same module again.

Of course, we still need a condition to stop the recursion. In the previous star code, we repeat similar tasks five times. The number of repetition is the stop condition, so the turtle_spiral module needs the times parameter. Every time the module complete its task, it subtracts one from times and invokes the same module again. That's why we execute turtle_spiral(t_after, times - 1, side_leng, angle, width) in the module.

Archimedean spiral

Besides forwarding a fixed length and turning a fixed angle, we can add some changes. For example, we can decrease step at next forwarding and stop the turtle when the length is smaller than a value.

// omitted..require turtle graphics implementation

module turtle_spiral(t_before, side_leng, d_step, min_leng, angle, width) {
    if(side_leng > min_leng) {
        t_after = forward(turn(t_before, angle), side_leng);
        polyline([get_xy(t_before), get_xy(t_after)], width);
        turtle_spiral(t_after, side_leng - d_step, d_step, min_leng, angle, width);
    }

}

side_leng = 50;
d_step = 1;
min_leng = 1;
angle = 90;
width = 1;

turtle_spiral(
    turtle(0, 0, 0), 
    side_leng, 
    d_step, 
    min_leng, 
    angle, 
    width
);

What will happen?

It looks like Archimedean spiral, right? In fact, using the following parameters will create an Archimedean spiral.

side_leng = 50;
d_step = 0.1;
min_leng = 1;
angle = 15;
width = 1;

As the first example shown in Archimedean spiral, the case here turns a fixed angle every time. However, why does the ray have the same length between two turnings? That's because we decrease a fixed length every time. It's easier to the relationship from the previous square model. It's shown below. You can see that the ray length between two turnings is always 2d.

So you can try to prove that the length between two turnings is always the same if the angle value is not less than 90.

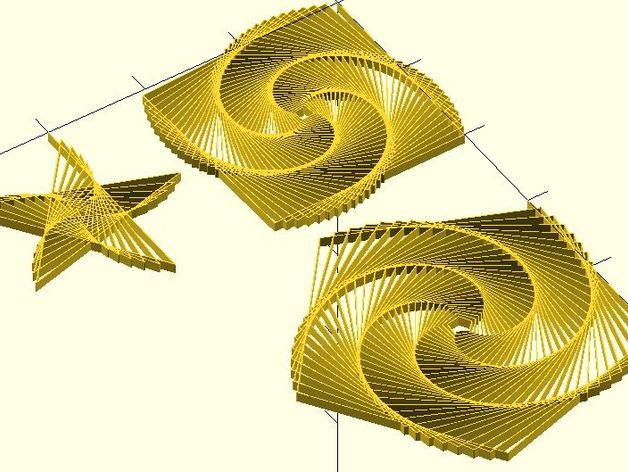
You may also try to use different parameters to draw models shown in the featured picture of Turtle Spiral Generator.

Golden spiral

By the way, you can also use turtle graphics to draw a golden spiral. It's more troublesome to deal with the forwarded length and the turned angle. It's an exercise for you. I only provide my solution here.

// omitted..require turtle graphics implementation

side_leng = 30;
min_leng = 0.2;
angle = 15;
width = 1;

module turtle_spiral_by_times(t_before, times, side_leng, angle, width) {
    if(times != 0) {
        t_after = forward(turn(t_before, angle), side_leng * angle / 180 * 3.14159);
        polyline([get_xy(t_before), get_xy(t_after)], width);

        turtle_spiral_by_times(t_after, times - 1, side_leng, angle, width);
    } else {
        turtle_spiral(t_before, side_leng / 1.618, min_leng, angle, width);
    }

}

module turtle_spiral(t_before, side_leng, min_leng, angle, width) {
    if(side_leng > min_leng) {
        times = 90 / angle;
        turtle_spiral_by_times(t_before, 90 / angle, side_leng, angle, width);
    }
}

turtle_spiral(
    turtle(0, 0, 0), 
    side_leng, 
    min_leng, 
    angle, 
    width
);

It draws a golden spiral indeed.